Introduction to knowledge graphs (section 5.4): Inductive knowledge – Symbolic learning

This article is section 5.4 of part 5 of the Introduction to knowledge graphs series of articles. Recent research has identified the development of knowledge graphs as an important aspect of artificial intelligence (AI) in knowledge management (KM).

In this section of their comprehensive tutorial article¹, Hogan and colleagues discuss two forms of symbolic learning for knowledge graphs: rule mining for learning rules and axiom mining for learning other forms of logical axioms.

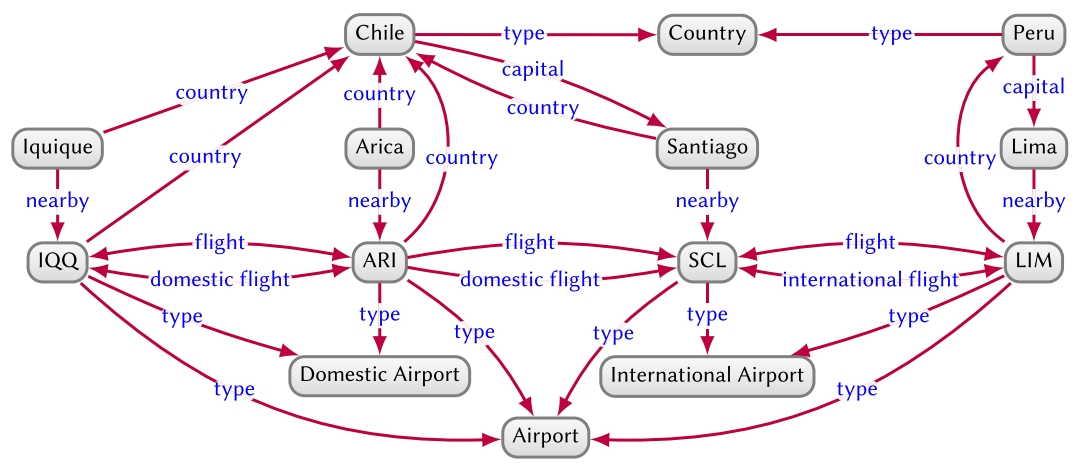
The supervised techniques discussed so far learn numerical models that are hard to interpret; for example, taking the graph of Figure 19, knowledge graph embeddings might predict the edge as being highly plausible, but the reason lies implicit in a complex matrix of learned parameters. Embeddings further suffer from the out-of-vocabulary problem, where they are often unable to provide results for inputs involving previously unseen nodes or edge-labels. An alternative is to use symbolic learning to learn hypotheses in a logical (symbolic) language that “explain” sets of positive and negative edges. Such hypotheses are interpretable; furthermore, they are quantified (e.g., “all airports are domestic or international”), partially addressing the out-of-vocabulary issue.

Rule Mining

Rule mining, in the general sense, refers to discovering meaningful patterns in the form of rules from large collections of background knowledge. In the context of knowledge graphs, we assume a set of positive and negative edges as given. The goal of rule mining is to identify new rules that entail a high ratio of positive edges from other positive edges, but entail a low ratio of negative edges from positive edges. The types of rules considered may vary from more simple cases, such as , to more complex rules, such as , indicating that airports near capitals tend to be international airports; or , indicating that flights within the same country denote domestic flights.

Per the international airport example, rules are not assumed to hold in all cases, but rather are associated with measures of how well they conform to the positive and negative edges. In more detail, we call the edges entailed by a rule and the set of positive edges (not including the entailed edge itself) the positive entailments of that rule. The number of entailments that are positive is called the support for the rule, while the ratio of a rule’s entailments that are positive is called the confidence for the rule. The goal is to find rules with both high support and confidence.

While similar tasks have been explored for relational settings with Inductive Logic Programming (ILP)², when dealing with an incomplete knowledge graph, it is not immediately clear how to define negative edges. A common heuristic is to adopt a Partial Completeness Assumption (PCA)³, which considers the set of positive edges to be those contained in the data graph.

An influential rule-mining system for graphs is AMIE⁴, which adopts the PCA measure of confidence and builds rules in a top-down fashion. For each such rule head, three types of refinements are considered, which add an edge with: (1) one existing variable and one fresh variable; (2) an existing variable and a node from the graph; (3) two existing variables. Combining refinements gives rise to an exponential search space that can be pruned. First, if a rule does not meet the support threshold, then its refinements need not be explored as refinements (1–3) reduce support. Second, only rules up to fixed size are considered. Third, refinement (3) is applied until a rule is closed, meaning that each variable appears in at least two edges of the rule (including the head); the previous rules produced by refinements (1) and (2) are not closed.

Later works have built on these techniques for mining rules from knowledge graphs. Gad-Elrab et al.⁵ propose a method to learn non-monotonic rules – rules with negated edges in the body – to capture exceptions to base rules. The RuLES system⁶ also learns non-monotonic rules and extends the confidence measure to consider the plausibility scores of knowledge graph embeddings for entailed edges not appearing in the graph. In lieu of PCA, the CARL system⁷ uses knowledge of the cardinalities of relations to find negative edges, while d’Amato et al.⁸ use ontologically entailed negative edges for measuring the confidence of rules generated by an evolutionary algorithm.

Another line of research is on differentiable rule mining, which enables end-to-end learning of rules by using matrix multiplication to encode joins in rule bodies. Along these lines, NeuralLP⁹ uses an attention mechanism to find variable-length sequences of edge labels for path-like rules. DRUM¹⁰ also learns path-like rules, where, observing that some edge labels are more/less likely to follow others, the system uses bidirectional recurrent neural networks (a technique for learning over sequential data) to learn sequences of relations for rules. These differentiable rule mining techniques are, however, currently limited to learning path-like rules.

Axiom Mining

Aside from rules, more general forms of axioms – expressed in logical languages such as Description Logics (DLs) – can be mined from a knowledge graph. We can divide these approaches into two categories: those mining specific axioms and more general axioms.

Among works mining specific types of axioms, disjointness axioms are a popular target; for example, the disjointness axiom DomesticAirport ⊓ InternationalAirport ≡ ⊥ states that the intersection of the two classes is equivalent to the empty class, i.e., no individual can be instances of both classes. Völker et al.¹¹ extract disjointness axioms based on (negative) association rule mining, which finds pairs of classes where each has many instances in the knowledge graph but there are relatively few (or no) instances of both classes. Töpper et al.¹² rather extract disjointness for pairs of classes that have a cosine similarity – computed over the nodes and edge-labels associated with a given class – below a fixed threshold. Rizzo et al.¹³ propose an approach that can further capture disjointness constraints between class descriptions (e.g., city without an airport nearby is disjoint from city that is the capital of a country) using a terminological cluster tree that first extracts class descriptions from clusters of similar nodes, and then identifies disjoint pairs of class descriptions.

Other systems propose methods to learn more general axioms. A prominent such system is DL-Learner¹⁴, which is based on algorithms for class learning (a.k.a. concept learning), whereby given a set of positive nodes and negative nodes, the goal is to find a logical class description that divides the positive and negative sets. Like AMIE, such class descriptions are discovered using a refinement operator used to move from more general classes to more specific classes (and vice versa), a confidence scoring function, and a search strategy. The system further supports learning more general axioms through a scoring function that determines what ratio of edges that would be entailed were the axiom true are indeed found in the graph; for example, to score the axiom ∃flight-.DomesticAirport ⊑ InternationalAirport over Figure 19, we can use a graph query to count how many nodes have incoming flights from a domestic airport (there are three), and how many nodes have incoming flights from a domestic airport and are international airports (there is one), where the greater the difference between both counts, the weaker the evidence for the axiom.

Next part: (part 6): Summary and conclusion.

Header image source: Crow Intelligence, CC BY-NC-SA 4.0.

References: