
Introduction to knowledge graphs (part 5): Inductive knowledge
This article introduces part 5 of the Introduction to knowledge graphs series of articles. Recent research has identified the development of knowledge graphs as an important aspect of artificial intelligence (AI) in knowledge management (KM).
In their comprehensive multi-author tutorial article1, Aidan Hogan and colleagues:
- outline graph data models and the languages used to query and validate them
- present deductive formalisms by which knowledge can be represented and entailed
- describe inductive techniques by which additional knowledge can be extracted.
Hogan and colleagues’ article is summarised in parts 3, 4, and 5 of this series, continuing with inductive knowledge in this part (part 5) as shown below. Additional information from other relevant reference sources has been added to some sections.
Tourism example
To keep the discussion accessible, Hogan and colleagues’ present concrete examples for a hypothetical knowledge graph, which are reproduced in the parts 3, 4, and 5 of this series. This hypothetical knowledge graph relates to tourism in Chile, aiming to increase tourism in the country and promote new attractions in strategic areas through an online tourist information portal. The knowledge graph itself will eventually describe tourist attractions, cultural events, services, businesses, as well as cities and popular travel routes.
Part 5 – Inductive knowledge
Inductive reasoning generalises patterns from input observations, which are used to generate novel but potentially imprecise predictions. For example, from a graph with geographical and flight information, we may observe that almost all capital cities of countries have international airports serving them, and hence predict that, since Santiago is a capital city, it likely has an international airport serving it; however, some capitals (e.g., Vaduz) do not have international airports. Predictions may thus have a level of confidence; for example, if we see that 187 of 195 capitals have an international airport, then we may assign a confidence of 0.959 for predictions made with that pattern. We then refer to knowledge acquired inductively as inductive knowledge, which includes both the models that encode patterns and the predictions made by those models.
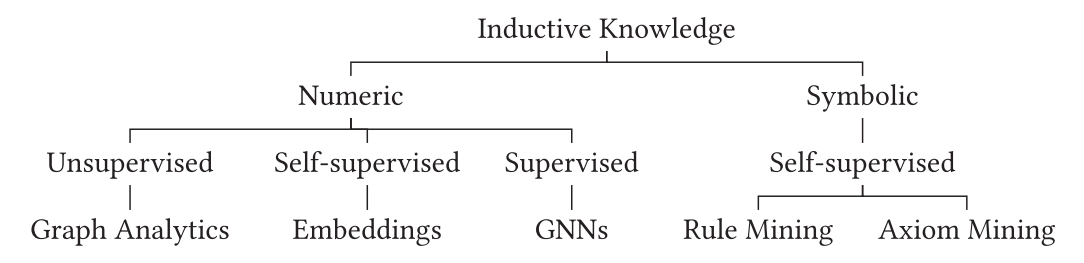
Inductive knowledge can be acquired from graphs using supervised or unsupervised methods. Supervised methods learn a function (a.k.a. model) to map a set of example inputs to their labelled outputs; the model can then be applied to unlabelled inputs. To avoid costly labelling, some supervised methods can generate the input–output pairs automatically from the (unlabelled) input, which are then fed into a supervised process to learn a model; herein, we refer to this approach as self-supervision. Alternatively, unsupervised processes do not require labelled input–output pairs, but rather apply a predefined function (typically statistical in nature) to map inputs to outputs.
In Figure 14, Hogan and colleagues provide an overview of the inductive techniques typically applied to knowledge graphs. In the case of unsupervised methods, there is a rich body of work on graph analytics, wherein well-known algorithms are used to detect communities or clusters, find central nodes and edges, and so on, in a graph. Alternatively, knowledge graph embeddings use self-supervision to learn a low-dimensional numerical model of elements of a knowledge graph. The structure of graphs can also be directly leveraged for supervised learning through graph neural networks. Finally, symbolic learning can learn symbolic models—i.e., logical formulae in the form of rules or axioms—from a graph in a self-supervised manner. We now discuss each of the aforementioned techniques in turn:
Section 5.2 – Knowledge graph embeddings
Section 5.3 – Graph neural networks
Section 5.4 – Symbolic learning
Next part: (section 5.1): Inductive knowledge – Graph analytics.
Header image source: Crow Intelligence, CC BY-NC-SA 4.0.
References:
- Hogan, A., Blomqvist, E., Cochez, M., d’Amato, C., Melo, G. D., Gutierrez, C., … & Zimmermann, A. (2021). Knowledge graphs. ACM Computing Surveys (CSUR), 54(4), 1-37. ↩



