
Introduction to knowledge graphs (section 4.1): Deductive knowledge – Ontologies
This article is section 4.1 of part 4 of the Introduction to knowledge graphs series of articles. Recent research has identified the development of knowledge graphs as an important aspect of artificial intelligence (AI) in knowledge management (KM).
Drawing on Hogan and colleagues’ comprehensive tutorial article1, this first section of the deductive knowledge part of the series introduces ontologies which constitute a formal representation of knowledge that, importantly, can be represented as a graph.
To enable entailment, there is a need to be precise about the meaning of the terms used. For example, the nodes “EID15” and “EID16” in Figure 1 have been referred to as “events.” But what if, for example, we wish to define two pairs of start and end dates for “EID16” corresponding to the different venues? Should we rather consider what takes place in each venue as a different event? What if an event has various start and end dates in a single venue: Would these be considered one (recurring) event or many events? These questions are facets of a more general question: What do we mean by an “event”? The term “event” may be interpreted in many ways, where the answers are a matter of convention.
In computing, an ontology is then a concrete, formal representation – a convention – on what terms mean within the scope in which they are used (e.g., a given domain). Like all conventions, the usefulness of an ontology depends on how broadly and consistently it is adopted and how detailed it is. Knowledge graphs that use a shared ontology will be more interoperable. Given that ontologies are formal representations, they can further be used to automate entailment.
Among the most popular ontology languages used in practice are the Web Ontology Language (OWL), recommended by the W3C and compatible with RDF graphs; and the Open Biomedical Ontologies Format (OBOF), used mostly in the biomedical domain. Since OWL is the more widely adopted, we focus on its features, though many similar features are found in both. Before introducing such features, however, we must discuss how graphs are to be interpreted.
Interpretations
We as humans may interpret the node “Santiago” in the data graph of Figure 1 as referring to the real-world city that is the capital of Chile. We may further interpret an edge ![]() as stating that there are flights from the city of Arica to this city. We thus interpret the data graph as another graph – what we here call the domain graph – composed of real-world entities connected by real-world relations. The process of interpretation, here, involves mapping the nodes and edges in the data graph to nodes and edges of the domain graph.
as stating that there are flights from the city of Arica to this city. We thus interpret the data graph as another graph – what we here call the domain graph – composed of real-world entities connected by real-world relations. The process of interpretation, here, involves mapping the nodes and edges in the data graph to nodes and edges of the domain graph.
We can thus abstractly define an interpretation of a data graph as the combination of a domain graph and a mapping from the terms (nodes and edge-labels) of the data graph to those of the domain graph. The domain graph follows the same model as the data graph. We refer to the nodes of the domain graph as entities and the edges of the domain graph as relations. Given a node “Santiago” in the data graph, we denote the entity it refers to in the domain graph (per a given interpretation) by ![]() . Likewise, for an edge
. Likewise, for an edge ![]() we will denote the relation it refers to by
we will denote the relation it refers to by ![]() . In this abstract notion of an interpretation, we do not require that “Santiago” or “Arica” be the real-world cities: An interpretation can have any domain graph and mapping.
. In this abstract notion of an interpretation, we do not require that “Santiago” or “Arica” be the real-world cities: An interpretation can have any domain graph and mapping.
Assumptions
Why is this abstract notion of interpretation useful? The distinction between nodes/edges and entities/relations becomes clear when we define the meaning of ontology features and entailment. To illustrate, if we ask whether there is an edge labelled “flight” between ![]() for the data graph in Figure 1, then the answer is no. However, if we ask if the entities
for the data graph in Figure 1, then the answer is no. However, if we ask if the entities ![]() are connected by the relation flight, then the answer depends on what assumptions we make when interpreting the graph. Under the Closed World Assumption (CWA) – which asserts that what is not known is assumed false – without further knowledge the answer is no. Conversely, under the Open World Assumption (OWA), it is possible for the relation to exist without being described by the graph. Under the Unique Name Assumption (UNA), which states that no two nodes can map to the same entity, we can say that the data graph describes at least two flights to “Santiago” (since “Viña del Mar” and “Arica” must be different entities). Conversely, under the No Unique Name Assumption (NUNA), we can only say that there is at least one such flight since “Viña del Mar” and “Arica” may be the same entity with two “names” (i.e., two nodes referring to the same entity).
are connected by the relation flight, then the answer depends on what assumptions we make when interpreting the graph. Under the Closed World Assumption (CWA) – which asserts that what is not known is assumed false – without further knowledge the answer is no. Conversely, under the Open World Assumption (OWA), it is possible for the relation to exist without being described by the graph. Under the Unique Name Assumption (UNA), which states that no two nodes can map to the same entity, we can say that the data graph describes at least two flights to “Santiago” (since “Viña del Mar” and “Arica” must be different entities). Conversely, under the No Unique Name Assumption (NUNA), we can only say that there is at least one such flight since “Viña del Mar” and “Arica” may be the same entity with two “names” (i.e., two nodes referring to the same entity).
These assumptions define which interpretations are valid and which interpretations satisfy which data graphs. The UNA forbids interpretations that map two nodes to the same entity, while the NUNA does not. Ontologies typically adopt the NUNA and OWA, i.e., the most general case, which considers that data may be incomplete, and two nodes may refer to the same entity.
Semantic Conditions
Beyond our base assumptions, we can associate certain patterns in the data graph with semantic conditions that define which interpretations satisfy it; for example, we can add a semantic condition on a special edge label “subp. of” (subproperty of) to enforce that if our data graph contains the edge ![]() , then any edge
, then any edge ![]() in the domain graph of the interpretation must also have a corresponding edge
in the domain graph of the interpretation must also have a corresponding edge ![]() to satisfy the data graph. These semantic conditions then form the features of an ontology language.
to satisfy the data graph. These semantic conditions then form the features of an ontology language.
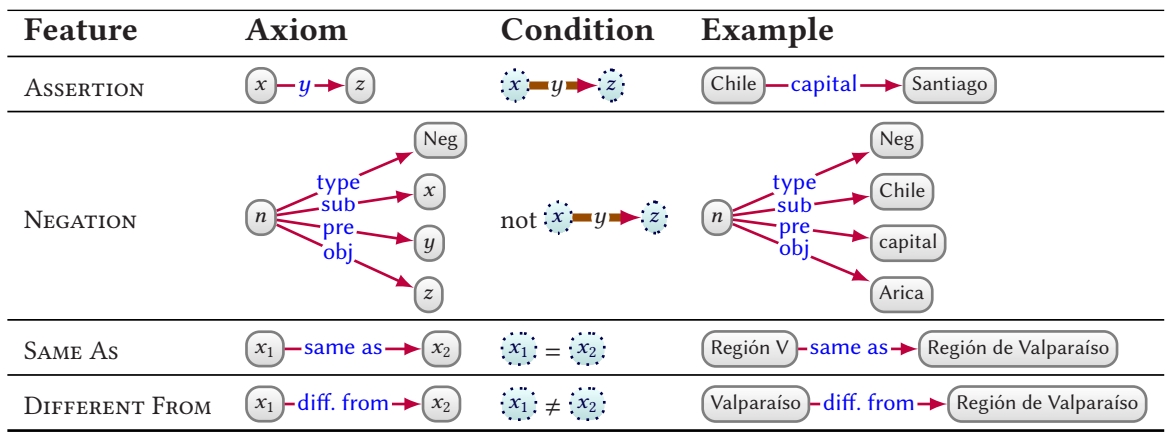
Individuals
Table 1 lists the main features supported by ontologies for describing individuals (a.k.a. entities). First, we can assert (binary) relations between individuals using edges such as ![]() . In the condition column, when we write
. In the condition column, when we write ![]() , for example, we refer to the condition that the given relation holds in the interpretation; if so, then the interpretation satisfies the assertion. We may further assert that two terms refer to the same entity, where, e.g.,
, for example, we refer to the condition that the given relation holds in the interpretation; if so, then the interpretation satisfies the assertion. We may further assert that two terms refer to the same entity, where, e.g., ![]() states that both refer to the same region; or that two terms refer to different entities, where, e.g.,
states that both refer to the same region; or that two terms refer to different entities, where, e.g., ![]() distinguishes the city from the region of the same name. We may also state that a relation does not hold using negation.
distinguishes the city from the region of the same name. We may also state that a relation does not hold using negation.
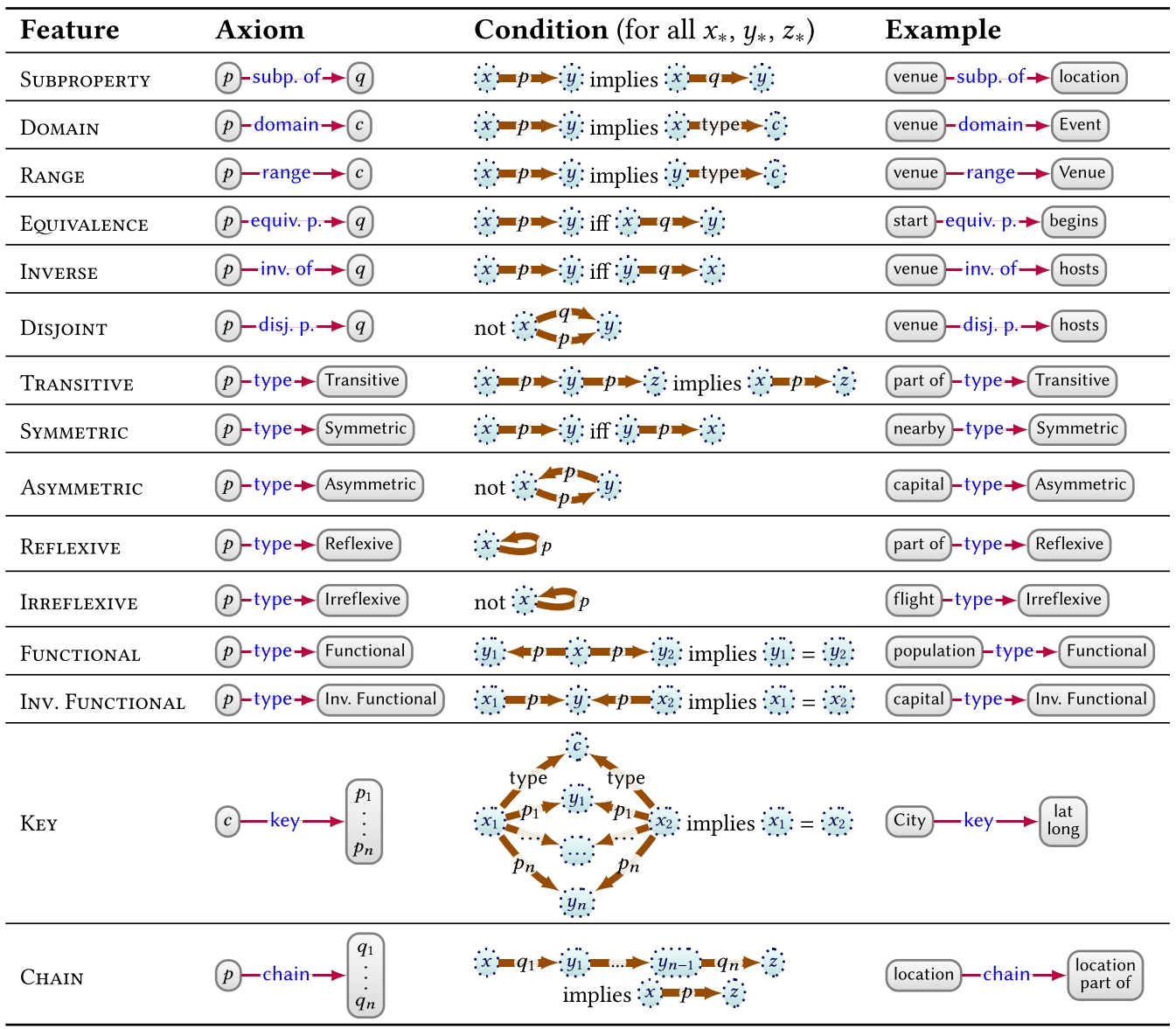
Properties
Properties denote terms that can be used as edge-labels. We may use a variety of features for defining the semantics of properties, as listed in Table 2. First, we may define subproperties as exemplified before. We may also associate classes with properties by defining their domain and range. We may further state that a pair of properties are equivalent, inverses, or disjoint, or define a particular property to denote a transitive, symmetric, asymmetric, reflexive, or irreflexive relation. We can also define the multiplicity of the relation denoted by properties, based on being functional (many-to-one) or inverse-functional (one-to-many). We may further define a key for a class, denoting the set of properties whose values uniquely identify the entities of that class. Without adopting a Unique Name Assumption (UNA), from these latter three features, we may conclude that two or more terms refer to the same entity. Finally, we can relate a property to a chain (a path expression only allowing concatenation of properties) such that pairs of entities related by the chain are also related by the given property. For the latter two features in Table 2, we use the vertical notation ![]() to represent lists (for example, OWL uses RDF lists).
to represent lists (for example, OWL uses RDF lists).
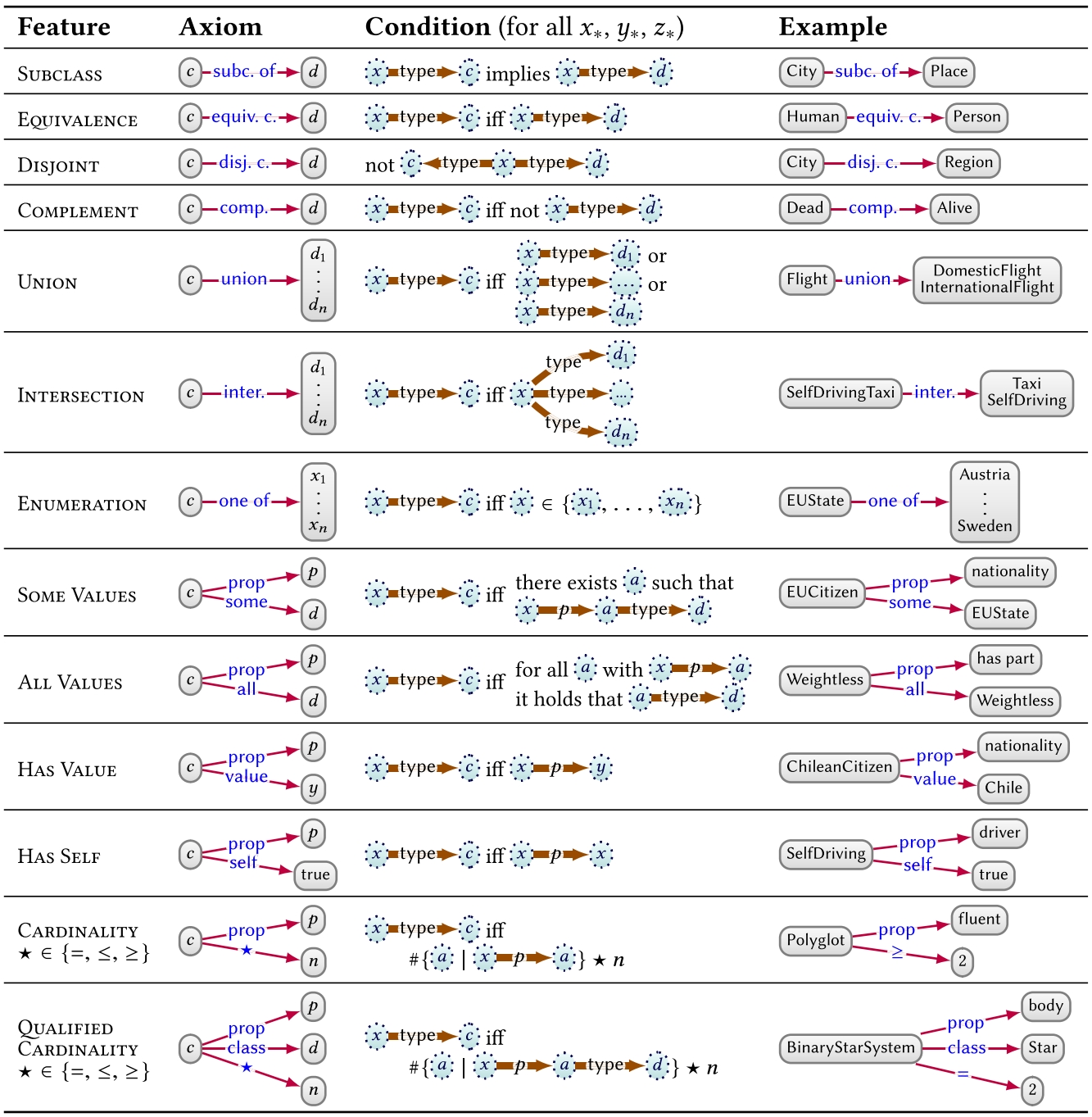
Classes
Often, we can group nodes in a graph into classes – such as Event, City, and so on – with a “type” property. Table 3 then lists a range of features for defining the semantics of classes. First, subclass can be used to define class hierarchies. We can further define pairs of classes to be equivalent or disjoint. We may also define novel classes based on set operators: as being the complement of another class, the union or intersection of a list of other classes, or as an enumeration of all of its instances. One can also define classes based on restrictions on the values its instances take for a property p, such as defining the class that has some value or all values from a given class on p; have a specific individual (has value) or themselves (has self) as a value on p; have at least, at most or exactly some number of values on p (cardinality); and have at least, at most or exactly some number of values on p from a given class (qualified cardinality). For the latter two cases, in Table 3, we use the notation ![]() to count distinct entities satisfying ϕ in the interpretation. Features can be combined to create complex classes, where combining the examples for INTERSECTION and HAS SELF in Table 3 gives the definition: self-driving taxis are taxis having themselves as a driver.
to count distinct entities satisfying ϕ in the interpretation. Features can be combined to create complex classes, where combining the examples for INTERSECTION and HAS SELF in Table 3 gives the definition: self-driving taxis are taxis having themselves as a driver.
Other Features
Ontology languages may support further features, including datatype vs. object properties, which distinguish properties that take datatype values from those that do not; and datatype facets, which allow for defining new datatypes by applying restrictions to existing datatypes, such as to define that places in Chile must have a float between -66.0 and -110.0 as their value for the (datatype) property “latitude.”
Next part (section 4.2): Deductive knowledge – Semantics and entailment.
Header image source: Crow Intelligence, CC BY-NC-SA 4.0.
References:
- Hogan, A., Blomqvist, E., Cochez, M., d’Amato, C., Melo, G. D., Gutierrez, C., … & Zimmermann, A. (2021). Knowledge graphs. ACM Computing Surveys (CSUR), 54(4), 1-37. ↩



