Equilibria and Stability Analysis: Introduction [Systems thinking & modelling series]

This is part 52 of a series of articles featuring the book Beyond Connecting the Dots, Modeling for Meaningful Results.

This section extends on our mathematical analysis of models by introducing the concepts of points of equilibria and stability analysis. These types of analyses allow you to determine many behaviors of a system without needing to fully solve its differential equation model.

Although the trajectory for the state variables in differential equation models generally cannot be determined analytically, several key properties of models can often still be determined. These properties include:

• The location of equilibrium points
• The stability of the equilibrium points

An equilibrium point is defined as a set of state variable values that will cause the system to cease changing. Once the system enters an equilibrium configuration, it will not leave that configuration without an external stimulus. For instance, in our exponential growth model a single equilibrium point exists: that of zero people. If the population is empty, then the population will not grow and instead remain at 0 indefinitely.

In the exponential growth population model there is only one equilibrium point (P = 0). In other models you may have multiple equilibrium points. In a model of a highly infectious, incurable disease you can imagine a system where two equilibrium points exist: one where no one is infected and a second point where everyone is infected. As long as there were no infectious individuals, the population would remain healthy. If just a single infected individual were introduced into the population, the infection would, however, spread until everyone was infected and the population would then remain at that point (remember this hypothetical disease is incurable).

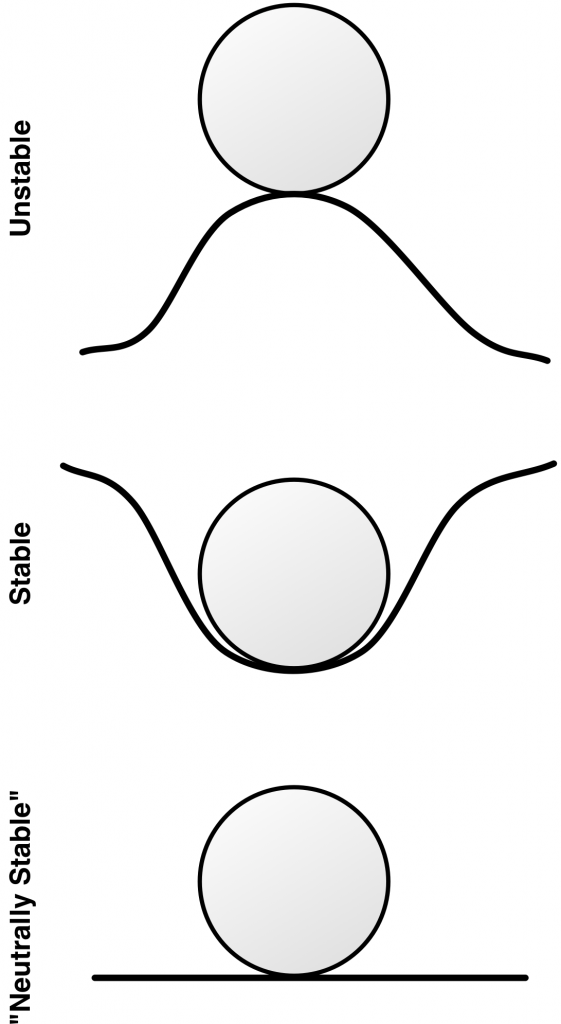
Multiple types of equilibria exist. Figure 1 illustrates what is known as the stability of equilibrium points. Each of the three panes in this figure shows a different form of equilibrium for the ball. In all three the balls are in equilibrium; if the no external forces come into play, the balls will not move. What differs in each of the three is what occurs if the balls are displaced by a small amount:

• Stable Equilibrium: In this type of equilibrium the ball will return to its original position if it is displaced. The structure of the system is such that the system is naturally attracted to the point of equilibrium. To use the physical metaphor, the equilibrium is at the bottom of a dip and the system naturally rolls into it.

• Unstable Equilibrium: Here the ball will move further and further away from the point of equilibrium if it is displaced by even a small amount. The equilibrium is unstable in that if we are just a small distance away from it, we move further away from it. To use the physical metaphor, the equilibrium is at the top of the hill and the system will move away from it unless it is placed at the exact point of equilibrium.

• “Neutrally Stable Equilibrium”: This is a less common form of equilibrium and goes by several different names. In this case if the ball is moved it will stay fixed at its new location. It will not move closer to or further from the original equilibrium. Of the three types of equilibrium, this one is of less interest or relevance in practice.

In the case of the highly infectious disease model, an equilibrium of everyone being healthy would be classified as an unstable equilibrium. The equilibrium would persist as long as no one brought the disease into the population (someone would not just spontaneously become ill), but if as little as a single sick person entered the population, the population would move further and further away from the equilibrium point of everyone being healthy and would never naturally return to it.

On the other hand, the equilibrium point of everyone being sick is a stable equilibrium, as no one recovers from the disease on their own. Even if you introduced healthy people into a population of sick individuals – moving the population away from the equilibrium – they too would eventually become sick, restoring the population to the equilibrium of everyone being sick.

Next edition: Equilibria and Stability Analysis: Equilibrium Points.

Article sources: Beyond Connecting the Dots, Insight Maker. Reproduced by permission.

Header image source: Beyond Connecting the Dots.